Research

Impact Mechanics of Composite Materials

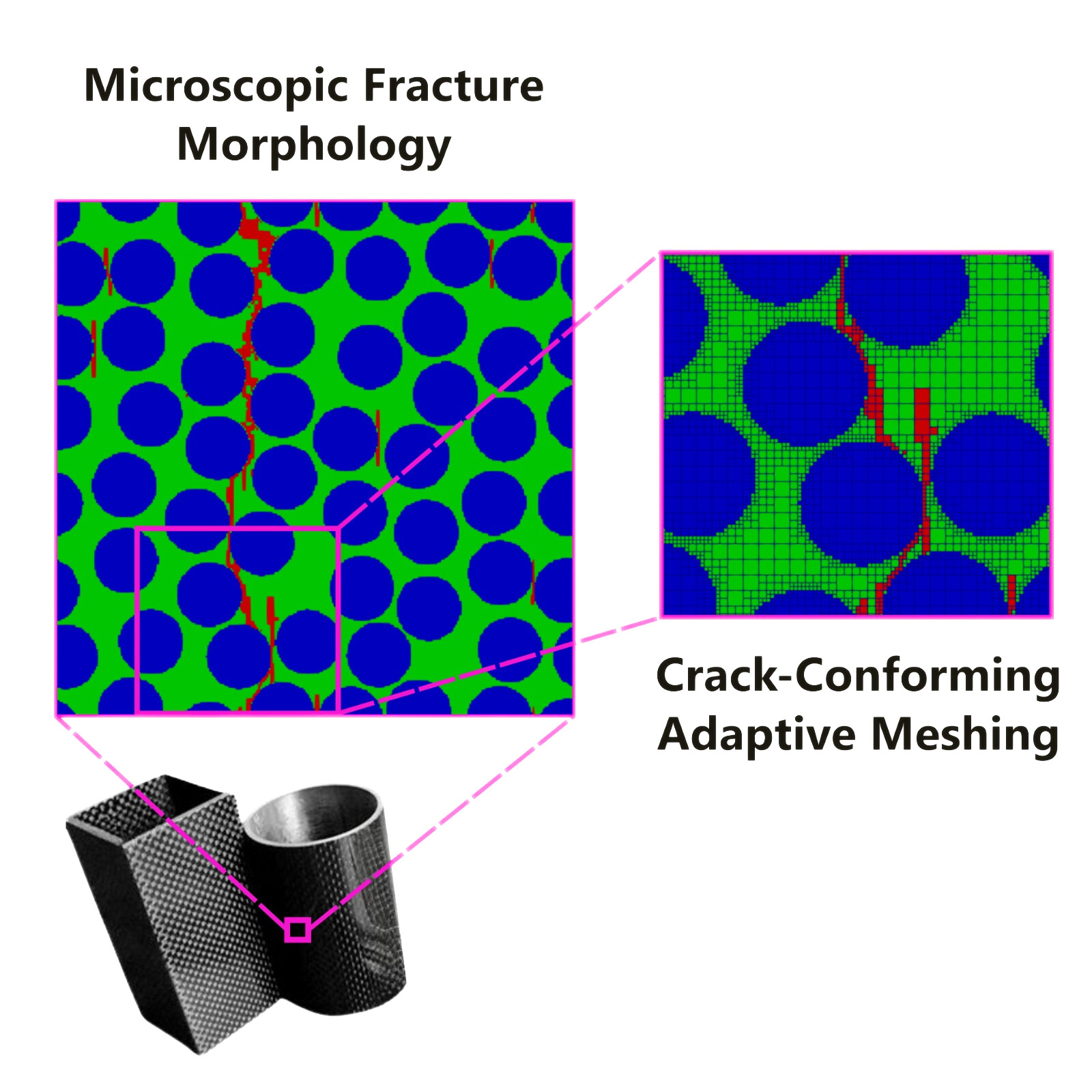
Our research focuses on building high-fidelity yet computationally efficient frameworks to predict the complex impact response of composite materials across all velocity regimes. For low-velocity impacts, we advance beyond conventional single-event studies to model both multi-site and repeated impact scenarios, capturing how impact energy, the number of strikes, and material recovery influence cumulative damage evolution. These effects are quantified using Gaussian Response Surface Methods in combination with advanced finite element models that incorporate our elasto-plastic damage and cohesive zone formulations. For high-velocity impacts, we develop analytical-computational approaches to explicitly solve wave propagation in layered media, supported by a custom wave-tracking code that resolves Riemann problems and provides insights into spall damage, interface debonding, and shock interactions. By integrating such high-fidelity simulations with reduced-order analytical and meta-models, our work delivers scalable, predictive tools that bridge constituent-level damage to structural failure, enabling the robust design of future impact-resistant composite systems.

Composite Modeling Across Scales

We aim to establish a seamless connection between material behaviors across length scales i.e. from microscale interactions to macroscale responses while significantly reducing the computational burden. Our research aims to advance predictive, physics-grounded, and computationally efficient structural-scale modeling of composites via multiscale approaches that link representative volume element (RVE) response to structural behavior to capture inelastic deformation, damage, and failure at low cost. Few routes to achieve this have been demonstrated in our prior work; we have developed reduced-order frameworks and Transformation Field Analysis (TFA) variants (including E²-TFA and D-TFA) that encode microscale inelasticity with damage evolution for homogenized response. Across scales, our models show consistency with practical results and reflect realistic damage progression and failure modes. We continue to extend these formulations toward anisotropic damage and interface damage, and we are also pursuing phase-field damage models for crack initiation/deflection/coalescence and heterogeneous interactions.

ML for Computaional Solid Mechanics

Machine learning is reshaping computational mechanics by advancing core areas such as constitutive modeling and multiscale analysis, particularly that of composite materials that exhibit plasticity, softening and fracture. By embedding the known physical principles into the learning process, Physics-Informed Neural Networks (PINNs) extend these capabilities even further offering models that not only learn on data but remain consistent with established physical laws. Our focus lies in developing an efficient PINN-based constitutive modeling framework that can be readily extended to multiscale analysis. By integrating the physical constraints with data driven insights, we envision PINN based model that accelerates the simulation of inelastic phenomenon in a reliable multiscale setting. Looking ahead, the future endeavors will be focused towards accurately capturing the overall softening as well as failure behaviors while overcoming the associated numerical and modeling difficulties, an area where current efforts remain limited. By tackling these challenges, we aim to advance PINNs as transformative tool in computational mechanics, delivering speed, flexibility and scalability beyond the reach of conventional approaches.

Geometric Modeling of Thin Materials

We investigate whether the characteristic shapes of thin laminae found in nature can be explained through the principles of mechanics, with the goal of applying their underlying physics to the design of thin structures. Thin materials are increasingly central to engineering, with applications spanning aircraft, bridges, ships, oil rigs, and storage vessels. A key phenomenon of interest is thin-sheet crumpling: when compressed along their boundaries, sheets do not deform smoothly but develop highly interconnected networks of ridges and vertices. In the vanishing thickness limit, these sheets behave as isometric surfaces that resist stretching while undergoing large deformations. Our research focuses on constructing developable surfaces that respect this isometry while capturing the interplay of bending and stretching energies. These models provide a rigorous mechanical foundation for the emergence of complex morphologies and enable predictive frameworks that connect naturally occurring laminae shapes with engineered thin-structure design. In doing so, we aim to advance both the fundamental understanding of crumpling and buckling and the development of lightweight, resilient structures for diverse engineering applications.